Point (geometry)

In geometry, topology and related branches of mathematics a spatial point describes a specific object within a given space that consists of neither volume, area, length, nor any other higher dimensional analogue. Thus, a point is a 0-dimensional object. Because of their nature as one of the simplest geometric concepts, they are often used in one form or another as the fundamental constituents of geometry, physics, vector graphics, and many other fields.

Contents

Points in Euclidean geometry

A finite set of points (blue) in two dimensional Euclidean space.

Points are most often considered within the framework of Euclidean geometry, where they are one of the fundamental objects. Euclid originally defined the point vaguely, as "that which has no part". In two dimensional Euclidean space, a point is represented by an ordered pair, 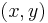\, (x,y), of numbers, where the first number conventionally represents the horizontal and is often denoted by 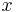\, x, and the second number conventionally represents the vertical and is often denoted by 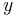\, y. This idea is easily generalized to three dimensional Euclidean space, where a point is represented by an ordered triplet, 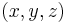\, (x,y,z), with the additional third number representing depth and often denoted by 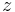\, z. Further generalizations are represented by an ordered tuplet of n terms,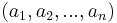\, (a_1,a_2,...,a_n) where n is the dimension of the space in which the point is located.

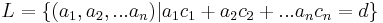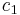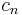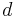Many constructs within Euclidean geometry consist of an infinite collection of points that conform to certain axioms. This is usually represented by a set of points; As an example, a line is an infinite set of points of the form \, L = \lbrace (a_1,a_2,...a_n)|a_1c_1 + a_2c_2 + ... a_nc_n = d \rbrace , where \, c_1 through \, c_n and \, d are constants and n is the dimension of the space. Similar constructions exist that define the plane, line segment and other related concepts.

In addition to defining points and constructs related to points, Euclid also postulated a key idea about points; he claimed that any two points can be connected by a straight line. This is easily confirmed under modern expansions of Euclidean geometry, and had lasting consequences at its introduction, allowing the construction of almost all the geometric concepts of the time. However, Euclid's postulation of points was neither complete nor definitive, as he occasionally assumed facts about points that didn't follow directly from his axioms, such as the ordering of points on the line or the existence of specific points. In spite of this, modern expansions of the system serve to remove these assumptions.

Points in branches of mathematics

A point in point-set topology is defined as a member of the underlying set of a topological space.

Although the notion of a point is generally considered fundamental in mainstream geometry and topology, there are some systems that forego it, e.g. noncommutative geometry and pointless topology. A “pointless space” is defined not as a set, but via some structure (algebraic or logical respectively) which looks like a well-known function space on the set: an algebra of continuous functions or an algebra of sets respectively. More precisely, such structures generalize well-known spaces of functions in a way that the operation “take a value at this point” may not be defined. A point is also a location and it has no size.

See also

External links